Hand Written Digits classification
Objective here is to develop a sequential model which can predict the hand written digits.
Dataset used: MNIST Dataset
Import required libraries and the dataset
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import tensorflow as tf
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import StratifiedKFold
#Loading Dataset
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
Visualise a sample of dataset
# Taking the sample from the dataset to visualize the content
print('Train: X=%s, y=%s' % (x_train.shape, y_train.shape))
print('Test: X=%s, y=%s' % (x_test.shape, y_test.shape))
# plot first few images
for i in range(9):
# define subplot
plt.subplot(330 + 1 + i)
# plot raw pixel data
plt.imshow(x_train[i], cmap=plt.get_cmap('gray'))
# show the figure
plt.show()
Train: X=(60000, 28, 28), y=(60000,)
Test: X=(10000, 28, 28), y=(10000,)

Data preprocessing
# Data present in the dataset is already quite normalized and pre-processed.
# However, we will further normalize it to make sure it uses less coomputational power.
# Normalize the training set
x_train = tf.keras.utils.normalize(x_train, axis=1)
# Normalize the testing set
x_test = tf.keras.utils.normalize(x_test, axis=1)
Sequential Model Building with Activation for each layer
Sequential model is the simplest model which uses a stack of layers.
We will build two different models with dirrent parameters to test which model gives better performance.
Model_v1: <ul> <li>Uses a single hidden layer with 64 units with ReLU as a activation function.</li>
<li>For regularization, we will use a Dropout of ratio 0.25 (This is done to avoid overfitting). </li>
<li>Batch Size would be 64 and optimizer will be Adam with learning rate 0.001 </li> </ul>
Model_v2: <ul> <li>Uses three hidden layer with 64,64,32 units with Sigmoid as a activation function.</li>
<li>For regularization, we will use both L2 Regularization(Factor: 0.0001) and Dropout of ratio 0.25 </li>
<li>Batch Size would be 256 and optimizer will be Stochastic Gradient Descent with learning rate 0.01 and momemtum 0.95 </li> </ul>
'''
Model_v1
'''
model_v1 = tf.keras.models.Sequential()
# Flattening the input.
model_v1.add(tf.keras.layers.Flatten())
# Input layer with activation function as 'ReLU'
model_v1.add(tf.keras.layers.Dense(64, activation=tf.nn.relu))
model_v1.add(tf.keras.layers.Dropout(0.25))
# First Hidden Layer(64 units) with Dropout regularization of ratio 0.25
model_v1.add(tf.keras.layers.Dense(64, activation=tf.nn.relu))
model_v1.add(tf.keras.layers.Dropout(0.25))
# Output Layer with 10 units( 0 - 9 )
model_v1.add(tf.keras.layers.Dense(10, activation=tf.nn.softmax))
'''
Model_v2
'''
model_v2 = tf.keras.models.Sequential()
# Flattening the input.
model_v2.add(tf.keras.layers.Flatten())
# Input layer with activation function as 'Sigmoid'
model_v2.add(tf.keras.layers.Dense(64, activation=tf.nn.sigmoid))
model_v2.add(tf.keras.layers.Dropout(0.25))
# First Hidden Layer(64 units) with Dropout regularization of ratio 0.25
model_v2.add(tf.keras.layers.Dense(64, activation=tf.nn.sigmoid,
kernel_regularizer=tf.keras.regularizers.l2(0.0001),
activity_regularizer=tf.keras.regularizers.l2(0.0001)))
model_v2.add(tf.keras.layers.Dropout(0.25))
# Second Hidden Layer(64 units) with Dropout regularization of ratio 0.25
model_v2.add(tf.keras.layers.Dense(64, activation=tf.nn.sigmoid,
kernel_regularizer=tf.keras.regularizers.l2(0.0001),
activity_regularizer=tf.keras.regularizers.l2(0.0001)))
model_v2.add(tf.keras.layers.Dropout(0.25))
# Third Hidden Layer(64 units) with Dropout regularization of ratio 0.25
model_v2.add(tf.keras.layers.Dense(32, activation=tf.nn.sigmoid,
kernel_regularizer=tf.keras.regularizers.l2(0.0001),
activity_regularizer=tf.keras.regularizers.l2(0.0001)))
model_v2.add(tf.keras.layers.Dropout(0.25))
# Output Layer with 10 units( 0 - 9 )
model_v2.add(tf.keras.layers.Dense(10, activation=tf.nn.softmax))
Compile with categorical CE loss and metric accuracy
Once we have build the model, we need to compile the model by adding some of the parameters which should feed information to the model on how to start the training process.
For model model_v1, we have used the Optimizer based on Adam Algorithm which uses learning rate of 0.001
For model model_v2, we have used the Stochastic gradient descent and momentum optimizer which uses learning rate of 0.001 and momentum of 0.95
model_v1.compile(optimizer = tf.keras.optimizers.Adam(learning_rate=0.001) ,
loss='sparse_categorical_crossentropy', metrics=["accuracy"])
model_v2.compile(optimizer = tf.keras.optimizers.SGD(learning_rate=0.01, momentum=0.95) ,
loss='sparse_categorical_crossentropy', metrics=["accuracy"])
Train Model with cross validation, with total time taken shown for 20 epochs
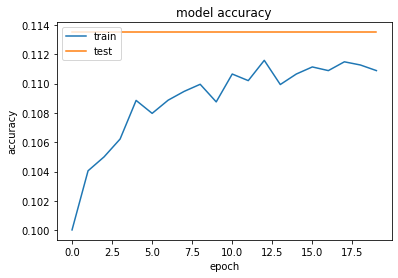
Model_v1 seems to be giving much more accuracy than model_v2, this is because in model_v1 we tried to avoid over-fitting by giving the Dropout. However with model_v2, with regularization and dropout, we have underfitted the model which has degraded the model’s accuracy.
'''
Fitting of Model_v1 with batch size as 64
'''
print("Fitting of Model_v1: \n")
model_v1_history = model_v1.fit(x_train, y_train,
batch_size=64,
epochs=20,
verbose=1,
validation_data=(x_test, y_test))
'''
Fitting of Model_v2 with batch size as 256
'''
print("Fitting of Model_v2: \n")
model_v2_history = model_v2.fit(x_train, y_train,
batch_size=256,
epochs=20,
verbose=1,
validation_data=(x_test, y_test))
Fitting of Model_v1:
Train on 60000 samples, validate on 10000 samples
Epoch 1/20
60000/60000 [==============================] - 6s 100us/sample - loss: 0.5567 - accuracy: 0.8311 - val_loss: 0.2029 - val_accuracy: 0.9385
Epoch 2/20
60000/60000 [==============================] - 4s 60us/sample - loss: 0.2657 - accuracy: 0.9218 - val_loss: 0.1548 - val_accuracy: 0.9533
Epoch 3/20
60000/60000 [==============================] - 4s 61us/sample - loss: 0.2146 - accuracy: 0.9383 - val_loss: 0.1375 - val_accuracy: 0.9591
Epoch 4/20
60000/60000 [==============================] - 4s 60us/sample - loss: 0.1851 - accuracy: 0.9454 - val_loss: 0.1261 - val_accuracy: 0.9631
Epoch 5/20
60000/60000 [==============================] - 4s 61us/sample - loss: 0.1663 - accuracy: 0.9506 - val_loss: 0.1189 - val_accuracy: 0.9642
Epoch 6/20
60000/60000 [==============================] - 4s 63us/sample - loss: 0.1558 - accuracy: 0.9542 - val_loss: 0.1141 - val_accuracy: 0.9672
Epoch 7/20
60000/60000 [==============================] - 4s 61us/sample - loss: 0.1435 - accuracy: 0.9568 - val_loss: 0.1130 - val_accuracy: 0.9675
Epoch 8/20
60000/60000 [==============================] - 4s 62us/sample - loss: 0.1314 - accuracy: 0.9597 - val_loss: 0.1094 - val_accuracy: 0.9686
Epoch 9/20
60000/60000 [==============================] - 4s 65us/sample - loss: 0.1277 - accuracy: 0.9612 - val_loss: 0.1058 - val_accuracy: 0.9683
Epoch 10/20
60000/60000 [==============================] - 4s 64us/sample - loss: 0.1187 - accuracy: 0.9645 - val_loss: 0.0976 - val_accuracy: 0.9703
Epoch 11/20
60000/60000 [==============================] - 4s 63us/sample - loss: 0.1154 - accuracy: 0.9646 - val_loss: 0.1004 - val_accuracy: 0.9702
Epoch 12/20
60000/60000 [==============================] - 4s 65us/sample - loss: 0.1094 - accuracy: 0.9658 - val_loss: 0.1011 - val_accuracy: 0.9705
Epoch 13/20
60000/60000 [==============================] - 4s 63us/sample - loss: 0.1054 - accuracy: 0.9676 - val_loss: 0.0978 - val_accuracy: 0.9720
Epoch 14/20
60000/60000 [==============================] - 4s 63us/sample - loss: 0.1025 - accuracy: 0.9681 - val_loss: 0.0976 - val_accuracy: 0.9719
Epoch 15/20
60000/60000 [==============================] - 4s 69us/sample - loss: 0.0980 - accuracy: 0.9706 - val_loss: 0.0922 - val_accuracy: 0.9741
Epoch 16/20
60000/60000 [==============================] - 4s 67us/sample - loss: 0.0988 - accuracy: 0.9684 - val_loss: 0.1044 - val_accuracy: 0.9718
Epoch 17/20
60000/60000 [==============================] - 5s 82us/sample - loss: 0.0948 - accuracy: 0.9697 - val_loss: 0.1000 - val_accuracy: 0.9731
Epoch 18/20
60000/60000 [==============================] - 5s 75us/sample - loss: 0.0919 - accuracy: 0.9717 - val_loss: 0.1011 - val_accuracy: 0.9728
Epoch 19/20
60000/60000 [==============================] - 5s 75us/sample - loss: 0.0909 - accuracy: 0.9719 - val_loss: 0.0956 - val_accuracy: 0.9718
Epoch 20/20
60000/60000 [==============================] - 5s 78us/sample - loss: 0.0849 - accuracy: 0.9736 - val_loss: 0.0965 - val_accuracy: 0.9738
Fitting of Model_v2:
Train on 60000 samples, validate on 10000 samples
Epoch 1/20
60000/60000 [==============================] - 6s 93us/sample - loss: 2.3728 - accuracy: 0.1000 - val_loss: 2.3225 - val_accuracy: 0.1135
Epoch 2/20
60000/60000 [==============================] - 2s 34us/sample - loss: 2.3287 - accuracy: 0.1041 - val_loss: 2.3222 - val_accuracy: 0.1135
Epoch 3/20
60000/60000 [==============================] - 2s 34us/sample - loss: 2.3264 - accuracy: 0.1050 - val_loss: 2.3214 - val_accuracy: 0.1135
Epoch 4/20
60000/60000 [==============================] - 2s 34us/sample - loss: 2.3244 - accuracy: 0.1062 - val_loss: 2.3212 - val_accuracy: 0.1135
Epoch 5/20
60000/60000 [==============================] - 2s 34us/sample - loss: 2.3233 - accuracy: 0.1089 - val_loss: 2.3207 - val_accuracy: 0.1135
Epoch 6/20
60000/60000 [==============================] - 2s 35us/sample - loss: 2.3230 - accuracy: 0.1080 - val_loss: 2.3206 - val_accuracy: 0.1135
Epoch 7/20
60000/60000 [==============================] - 2s 35us/sample - loss: 2.3221 - accuracy: 0.1089 - val_loss: 2.3204 - val_accuracy: 0.1135
Epoch 8/20
60000/60000 [==============================] - 2s 35us/sample - loss: 2.3215 - accuracy: 0.1095 - val_loss: 2.3198 - val_accuracy: 0.1135
Epoch 9/20
60000/60000 [==============================] - 2s 33us/sample - loss: 2.3214 - accuracy: 0.1099 - val_loss: 2.3198 - val_accuracy: 0.1135
Epoch 10/20
60000/60000 [==============================] - 2s 35us/sample - loss: 2.3212 - accuracy: 0.1088 - val_loss: 2.3192 - val_accuracy: 0.1135
Epoch 11/20
60000/60000 [==============================] - 2s 35us/sample - loss: 2.3204 - accuracy: 0.1107 - val_loss: 2.3191 - val_accuracy: 0.1135
Epoch 12/20
60000/60000 [==============================] - 2s 35us/sample - loss: 2.3200 - accuracy: 0.1102 - val_loss: 2.3193 - val_accuracy: 0.1135
Epoch 13/20
60000/60000 [==============================] - 2s 33us/sample - loss: 2.3198 - accuracy: 0.1116 - val_loss: 2.3186 - val_accuracy: 0.1135
Epoch 14/20
60000/60000 [==============================] - 2s 33us/sample - loss: 2.3195 - accuracy: 0.1099 - val_loss: 2.3183 - val_accuracy: 0.1135
Epoch 15/20
60000/60000 [==============================] - 2s 34us/sample - loss: 2.3190 - accuracy: 0.1107 - val_loss: 2.3182 - val_accuracy: 0.1135
Epoch 16/20
60000/60000 [==============================] - 2s 37us/sample - loss: 2.3188 - accuracy: 0.1111 - val_loss: 2.3179 - val_accuracy: 0.1135
Epoch 17/20
60000/60000 [==============================] - 2s 34us/sample - loss: 2.3183 - accuracy: 0.1109 - val_loss: 2.3173 - val_accuracy: 0.1135
Epoch 18/20
60000/60000 [==============================] - 2s 33us/sample - loss: 2.3182 - accuracy: 0.1115 - val_loss: 2.3170 - val_accuracy: 0.1135
Epoch 19/20
60000/60000 [==============================] - 2s 33us/sample - loss: 2.3181 - accuracy: 0.1113 - val_loss: 2.3167 - val_accuracy: 0.1135
Epoch 20/20
60000/60000 [==============================] - 2s 34us/sample - loss: 2.3178 - accuracy: 0.1109 - val_loss: 2.3166 - val_accuracy: 0.1135
Visualise Loss and Accuracy history
# Lets see the predictions of model_v1 for a sample set.
plt.imshow(x_test[1000],cmap='gray')
plt.title("Digit at 1000th sample:")
plt.show()
predictions_v1 = model_v1.predict([x_test])
print("Predicted by model_v1: ",np.argmax(predictions_v1[1000]))
predictions_v2 = model_v2.predict([x_test])
print("Predicted by model_v2: ",np.argmax(predictions_v2[1000]))
'''
For Model_v1
'''
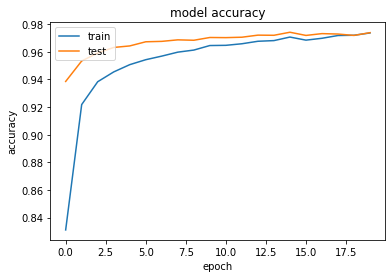
# summarize history for accuracy
plt.plot(model_v1_history.history['accuracy'])
plt.plot(model_v1_history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
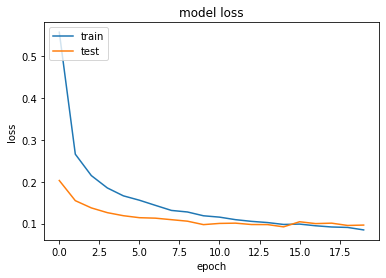
# summarize history for loss
plt.plot(model_v1_history.history['loss'])
plt.plot(model_v1_history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
'''
For Model_v2
'''
# summarize history for accuracy
plt.plot(model_v2_history.history['accuracy'])
plt.plot(model_v2_history.history['val_accuracy'])
plt.title('model accuracy')
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
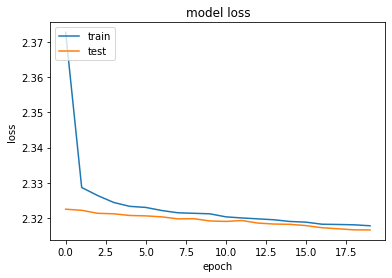
# summarize history for loss
plt.plot(model_v2_history.history['loss'])
plt.plot(model_v2_history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
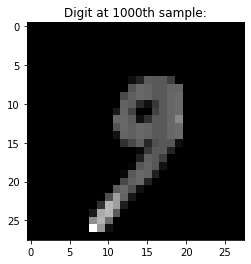
Predicted by model_v1: 9
Predicted by model_v2: 1
Show Confusion Matrix for validation dataset
predictions_cls_v1 = model_v1.predict_classes([x_test])
predictions_cls_v2 = model_v2.predict_classes([x_test])
cm_v1 = confusion_matrix(y_test, predictions_cls_v1)
cm_v2 = confusion_matrix(y_test, predictions_cls_v2)
'''
For Model_v1
'''
plt.imshow(cm_v1, cmap=plt.cm.Blues)
plt.xlabel("Predicted labels")
plt.ylabel("True labels")
plt.xticks([0,1,2,3,4,5,6,7,8,9], [0,1,2,3,4,5,6,7,8,9])
plt.yticks([0,1,2,3,4,5,6,7,8,9], [0,1,2,3,4,5,6,7,8,9])
plt.title('Confusion matrix for Model_v1')
plt.colorbar()
plt.show()
'''
For Model_v2
'''
plt.imshow(cm_v2, cmap=plt.cm.Blues)
plt.xlabel("Predicted labels")
plt.ylabel("True labels")
plt.xticks([0,1,2,3,4,5,6,7,8,9], [0,1,2,3,4,5,6,7,8,9])
plt.yticks([0,1,2,3,4,5,6,7,8,9], [0,1,2,3,4,5,6,7,8,9])
plt.title('Confusion matrix for Model_v2')
plt.colorbar()
plt.show()


Summary
Above results shows that the Model_v1 provides great prediction however Model_v2 has worst performance. Reason behind it that we have underfitted the model by using multiple regularizations while fitting the model which has resulted in the worst performance.